2017国家公务员行测备考：图形推理解题思路

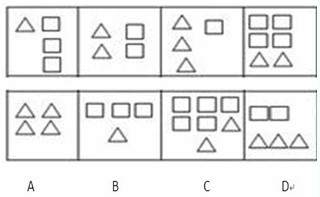
	换算类的图形推理题，应该是图形中难度较大的一种，出题的数量不会很多，但是一般的考生遇到这类题，很少能够快速解题，或者有时也就想不到会考察它。提醒广大考生，换算类的图形题，它题目的特点是，题干中的图形一般都包含两个不同的元素，单独看它的数量没有规律，需要将两个元素结合在一起看，并且两者之间存在一个换算的关系。 　　我们重点就来看一下，能否从一个严谨的数学的角度来进行一个解析。举个例子来讲： 　　【例】 　　图形中包含两个元素：三角形和方块，单独看每一个元素没有严谨的数量规律，所以我们需要将两个元素结合在一起看规律。在以往的考试中，元素替代后呈现等差数列的题目占了绝大多数，所以我们在做题的时候也主要从等差数列的角度来看。 　　【思路一】看图形中重叠最多的两幅图 　　很明显的第一幅图和第二幅图，都有两个方块和一个三角形，把重叠的部分划掉，第一幅剩下一个方块，第二幅图只剩下一个三角形，要想使之呈现一个简易的等差数列，只要1个三角形=2个方块就可以了。整理一下方块的个数，数量规律是5,6,7,8?所以选择C。 　　【思路二】列等差数列的公式 　　我们知道，绝大部分的换算题都是一个等差的数量，那么我们就从严谨的公式中去解出三角形和方块的一个数量上的关系。我们假定三角形为x，方块为y。数学中的等差中项即等差数列头尾两项的和的一半。将后三幅图联系在一起，第二幅图为(2x+2y);第三幅为(3x+y);第四幅为(2x+4y)，根据等差中项公式得到：(2x+2y)+(2x+4y)=2(3x+y)，解二元一次方程得到x=2y，即三角形=2方块，亦可以得到答案选择C。 　　两个思路都可以解题，思路一方法简单做题速度快，但是严谨性不高，思路二我们从数学的视角来分析，虽然可以准确得到答案，但是需要花费一定的时间，所以在各位考生在备考过程中要多加练习，结合自身特点，选择适合自己的方法，如果两个方法都学会那就更好了。